周波数領域?ふーん。なるほどー。(移動平均でいいじゃん。)
そんな方向けにローパスフィルタについてまとめてみます。
まずはフーリエ変換の雰囲気をつかむ
ローパスフィルタを知るにはまず「フーリエ変換」を(雰囲気だけでも)知っておく必要があります。
ネットで調べれば下の図のような説明は多く見かけるでしょう。
しかし物事を理解するには歴史、背景、目的みたいなものを多少でも知ることが大事だと思うのです。
フーリエ変換 = 時系列信号を周波数成分(sin波)に分解する変換
ですが、そもそもなぜこんな変換を昔の人はしたかったのか。
その起源は波動にあります。
例えば音。子供しか聞こえないモスキート音は「周波数が高い」。
あるいは光。紫外線は「波長が短い」。
ラジオなど無線にも「周波数帯」なるものがある。
この世のいろんな信号は「波」に変換され「周波数」なるもので表現されています。
この世のあらゆる信号は波に変換できる(仮)。その変換こそがフーリエ変換なわけで。

上のgifは少し前にtwitterで回ってました。
いろんな周期の波を足せばどんな信号も表現できるのです。
こうして信号をフーリエ変換すると、どの周波数がどれだけ含まれているか、というヒストグラムが出ます。
左を時間領域、右を周波数領域、と表現したりもします。
ではなぜこんな変換をするのか。答えは「ノイズ」です。
一番わかりやすいのは音。イヤホンやラジオの音質は大事ですよね。
あるいは光。UVカットサングラス、はどうやってカットしてるんでしょう??
欲しい信号だけ通して、いらない信号はカットする。それが「フィルタ」であり、
例えば高い周波数のノイズをカットするのが「ローパスフィルタ」なわけです。
次に伝達関数の雰囲気をつかむ
このフーリエ変換、制御的にとても嬉しい点が一つあります。
それは、周波数領域は時間に依存しない表現ができること。
つまり定常状態を表現できるわけです!
例えば車のハンドルを右に切った時。
車がどれくらい遅れて、どれくらい右に動くかを一つの数式で表現できます。
これって実はめちゃめちゃすごいことで、
本当はハンドルを切る時間とか量によって時間領域の信号は毎回違うわけです。
でもそんなの関係ねぇ!という物理的なモデル構築がフーリエ様によって可能になったわけです。
一つの数式(=モデル=伝達関数)で、ハンドルから車までを表現できる。
フーリエ変換のおかげでモデルベース制御なるものが生まれたわけですね。
(雰囲気説明なので多少の誤りはお許しを)
ローパスフィルタの伝達関数
ローパスフィルタはwikipediaを見ての通り、電気系が起源です。
電気信号はとにかくノイズ(高い周波数の不要な信号)が多いので、それを除去したいと。
以下にローパスフィルタの伝達関数を示します。
この図のτ(タウ)を時定数とか呼びます。
時定数の逆数をcut-off frequency(遮断周波数)とか呼びます。
とかそんなことはどうでもよくて。
大事なのは上図の下側、等価変換です。
伝達関数を書けても実装できなければつまらない。実装しやすくするために伝達関数を変換することも時には必要なのです。
上図を式にするとoutput = input / (1+sτ)
output * (1+sτ) = input
output = (input - output) / sτ
という具合に等価変換できます。
1/sが積分?なぜ??という方はぜひラプラス変換をもっと勉強してみましょう。
そんなわけでローパスフィルタをpythonで実装すると...
一行で完結。
output = (input - output) / sτ
cut_f = 1/τなので cut_f * (input - output)を積分しています。
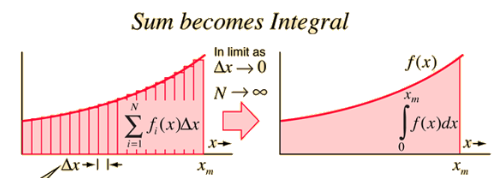
積分ってそうやって実装するの?という方は下図を見て納得しましょう。
(もちろん他にも実装方法はあります)
おわりに
知人に「ローパスとは」って聞かれて参考リンクでも送ろうと思ってググったら、けっこう敷居の高い記事が多いんですね。社会人になってから知らない分野を勉強するのってやっぱ大変なんだなぁ。自分もちゃんと手計算で等価変換とかしたのは院生になってからだし。ちなみにハイパスはsτ/(1+sτ)でローパスと足すと1になるんですよ。
おしまい。